Baekjoon/G4/2636. 치즈

G4) 2636. 치즈

문제

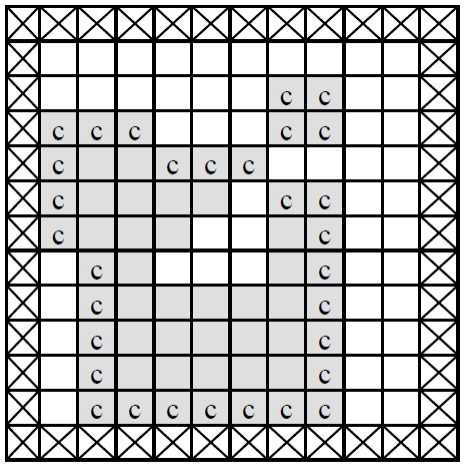
아래 그림 1과 같이 정사각형 칸들로 이루어진 사각형 모양의 판이 있고, 그 위에 얇은 치즈(회색으로 표시된 부분)가 놓여 있다. 판의 가장자리(그림 1에서 네모 칸에 X친 부분)에는 치즈가 놓여 있지 않으며 치즈에는 하나 이상의 구멍이 있을 수 있다.

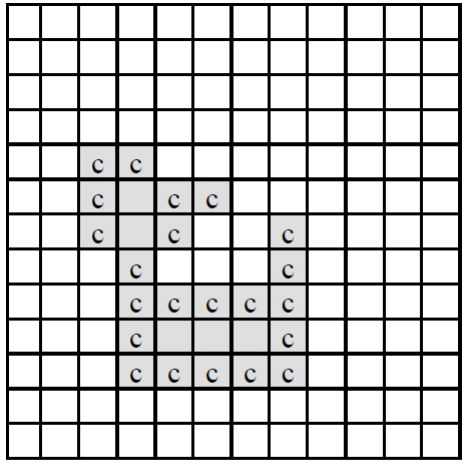
이 치즈를 공기 중에 놓으면 녹게 되는데 공기와 접촉된 칸은 한 시간이 지나면 녹아 없어진다. 치즈의 구멍 속에는 공기가 없지만 구멍을 둘러싼 치즈가 녹아서 구멍이 열리면 구멍 속으로 공기가 들어가게 된다. 그림 1의 경우, 치즈의 구멍을 둘러싼 치즈는 녹지 않고 ‘c’로 표시된 부분만 한 시간 후에 녹아 없어져서 그림 2와 같이 된다.

(그림 1)

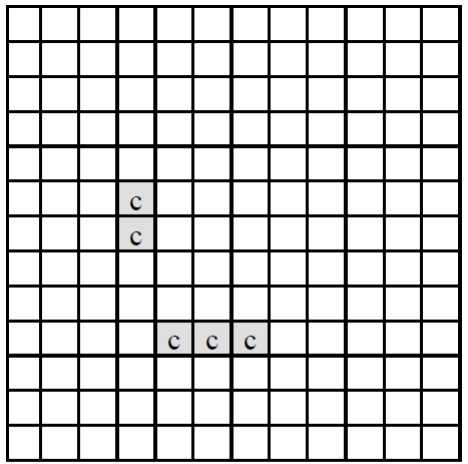
다시 한 시간 후에는 그림 2에서 ‘c’로 표시된 부분이 녹아 없어져서 그림 3과 같이 된다.

(그림 2) (그림 3)

그림 3은 원래 치즈의 두 시간 후 모양을 나타내고 있으며, 남은 조각들은 한 시간이 더 지나면 모두 녹아 없어진다. 그러므로 처음 치즈가 모두 녹아 없어지는 데는 세 시간이 걸린다. 그림 3과 같이 치즈가 녹는 과정에서 여러 조각으로 나누어 질 수도 있다.

입력으로 사각형 모양의 판의 크기와 한 조각의 치즈가 판 위에 주어졌을 때, 공기 중에서 치즈가 모두 녹아 없어지는 데 걸리는 시간과 모두 녹기 한 시간 전에 남아있는 치즈조각이 놓여 있는 칸의 개수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에는 사각형 모양 판의 세로와 가로의 길이가 양의 정수로 주어진다. 세로와 가로의 길이는 최대 100이다. 판의 각 가로줄의 모양이 윗 줄부터 차례로 둘째 줄부터 마지막 줄까지 주어진다. 치즈가 없는 칸은 0, 치즈가 있는 칸은 1로 주어지며 각 숫자 사이에는 빈칸이 하나씩 있다.

출력

첫째 줄에는 치즈가 모두 녹아서 없어지는 데 걸리는 시간을 출력하고, 둘째 줄에는 모두 녹기 한 시간 전에 남아있는 치즈조각이 놓여 있는 칸의 개수를 출력한다.

풀이

BFS를 활용한 구현 문제였다.

판의 각 칸들은 0 - 구멍, 1 - 치즈, 2 - 공기의 3가지 상태를 가진다.

맨 처음 칸의 가장자리에서 그래프 탐색을 이용하여 치즈 외부 구멍들을 전부 공기 상태로 만들어 준 다음, 판에서 치즈가 사라질 때 까지 공기와 인접한 치즈들을 전부 구멍으로 만들고, 공기와 인접한 구멍들을 전부 공기로 만든다.

코드

import java.util.*;
import java.io.*;

public class Main {
	static int N, M, prev, t, num;
	static int[][] cheese;
	static Queue<int[]> queue;
	static int[] dy = {-1, 1, 0, 0};
	static int[] dx = {0, 0, -1, 1};
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringTokenizer st = new StringTokenizer(br.readLine());

		N = Integer.parseInt(st.nextToken());
		M = Integer.parseInt(st.nextToken());

		cheese = new int[N][M];
		queue = new LinkedList<>();

		for (int i = 0; i < N; i++) {
			st = new StringTokenizer(br.readLine());

			for (int j = 0; j < M; j++) {
				cheese[i][j] = Integer.parseInt(st.nextToken());
				if (cheese[i][j] == 1) {
					num++;
				}
			}
		}

		cheese[0][0] = 2;
		queue.add(new int[] {0, 0});
		while (!queue.isEmpty()) {
			int[] cur = queue.poll();

			for (int i = 0; i < 4; i++) {
				int ny = cur[0] + dy[i];
				int nx = cur[1] + dx[i];

				if (ny >= 0 && nx >= 0 && ny < N && nx < M && cheese[ny][nx] == 0) {
					cheese[ny][nx] = 2;
					queue.add(new int[] {ny, nx});
				}
			}
		}
		/*
		 * 2로 채움
		 * 2근처 1을 0으로 바꾸기
		 * 2근처 0을 2로 바꾸기
		 * 1이 사라질 때 까지 2를 반복
		 * 1이 사라지면 직전 값 출력
		 */
		while (true) {
			t++;
			prev = num;
			for (int i = 1; i < N - 1; i++) {
				for (int j = 1; j < M - 1; j++) {
					if (cheese[i][j] == 1 && (cheese[i - 1][j] == 2 || cheese[i + 1][j] == 2 || cheese[i][j - 1] == 2 || cheese[i][j + 1] == 2)) {
						cheese[i][j] = 0;
						num--;
					}
				}
			}
			if (num == 0) {
				break;
			}
			for (int i = 1; i < N - 1; i++) {
				for (int j = 1; j < M - 1; j++) {
					if (cheese[i][j] == 0 && (cheese[i - 1][j] == 2 || cheese[i + 1][j] == 2 || cheese[i][j - 1] == 2 || cheese[i][j + 1]== 2)) {
						cheese[i][j] = 2;
						queue.add(new int[] {i, j});
						while (!queue.isEmpty()) {
							int[] cur = queue.poll();

							for (int k = 0; k < 4; k++) {
								int ny = cur[0] + dy[k];
								int nx = cur[1] + dx[k];

								if (ny > 0 && nx > 0 && ny < N - 1 && nx < M - 1 && cheese[ny][nx] == 0) {
									cheese[ny][nx] = 2;
									queue.add(new int[] {ny, nx});
								}
							}
						}
					}
				}
			}
		}
		bw.write(t + "\n" + prev + "\n");
		bw.flush();
		br.close();
		bw.close();
	}

}